A sequence is an order of numbers that follow a pattern, whatever that may be e.g. a times table. An arithmetic sequence is a sequence where the distance between each number remains the same.
For example, look at the following sequence - 3, 5, 7 and 9. There is a gap of two between every number. To continue the arithmetic sequence, we simply need to add two to the last number: 11, 13, 15 and so on.
The arithmetic sequence is very common in Maths - it is a topic in AQA, Edexcel and OCR exams. We will explore the key terms, including the common difference, formulas to help navigate these sequences, and common questions related to this topic. Quizzes will be provided throughout the article to test your knowledge. If you need more help, you can search for a maths GCSE tutor for lessons.
The nth term is the name/rule that the sequence follows to create an ordered list of numbers. It will feature heavily in this article.
The common difference
Each number in a sequence is called a "term". We will refer to each number as a term in this article.
The common difference means the shared distance between each consecutive term in an arithmetic sequence. If we have the sequence, 2, 4, 6, 8, then the common difference is 2.
The common difference never changes in an arithmetic sequence and will always remain the same.
It's important to bear in mind that we can add or subtract the common difference in an arithmetic sequence. For example, in this sequence 3, -1, -5, -9, the common difference is -4.
We are told how to move from one term to the next using the term-to-term rule. Here are a few examples:
- The first term is 5
- The term-to-term rule is to subtract 4
- The first four terms are 5, 1, -3, -7
- The first term is 3
- The term-to-term rule is to add 10
- The first four terms are -3, 7, 17, 27
- The first term is 4 1/2
- The term-to-term rule is to subtract 3/4
- The first four terms are 3 3/4, 3, 2 1/4, 1 1/2
Arithmetic sequences are also known as linear sequences. Linear means straight and if we were to represent an arithmetic sequence visually, it would show a straight line going up or down. For example, take the graph below:
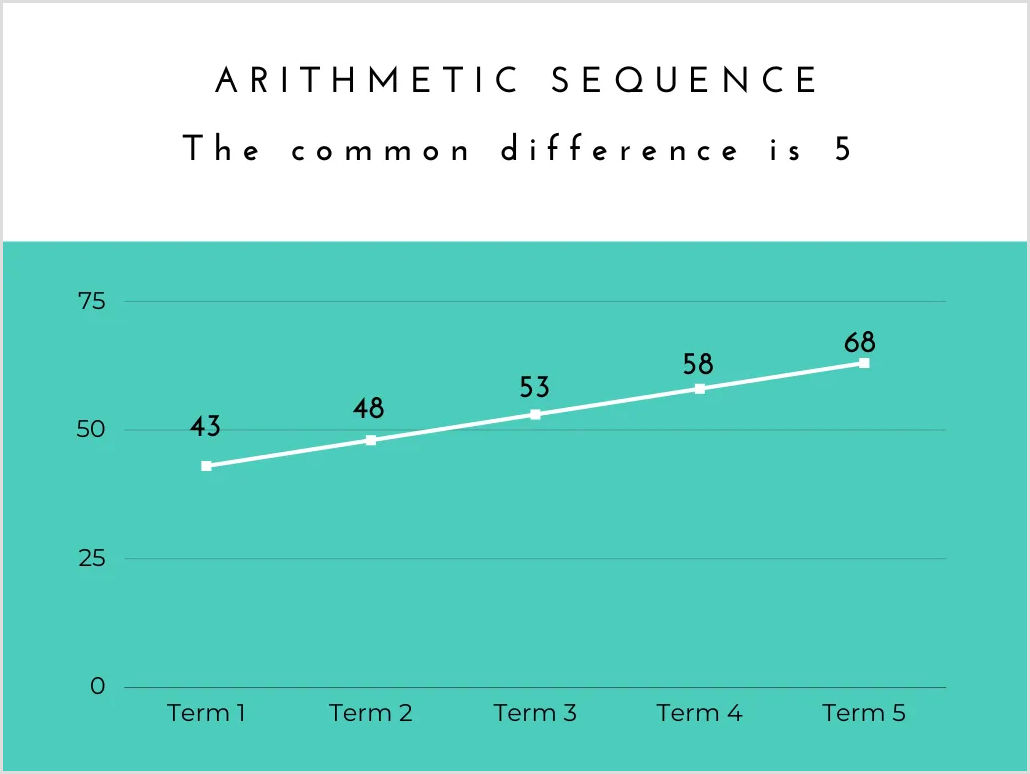
An arithmetic sequence can also be called an arithmetic progression. You can use these terms interchangeably. We will use the former term for this article.
The arithmetic sequence formula
Finding the terms of an arithmetic sequence in Maths has so far been fairly straightforward. However, what if you're asked to find the sum of the first 50 terms? What if the common difference is an awkward value, such as being especially large or a fraction?
This is where the arithmetic sequence formula comes in. Formulas are designed to be used when the manual process is impractical:
an = a1 + (n-1)d
We can use this formula to find the nth term. Put another way, this calculation will find any term in a sequence. It is also known as the general term of the arithmetic sequence.
Let's break down the terms in the formula:
- an is the nth term (general term)
- a1 is the first term
- n is the term position
- d is the common difference
We can now apply this step by step to the sequence below:
5 - 12 - 19 - 26 - 33
- The first term is 5, so a1 = 5
- The common difference between each term is 7, so d = 7
- Now we know the common difference and first term, we can use the formula above to find any term in the arithmetic sequence.
- For example, if we need to find the 15th coefficient, the calculation is: 715 = 5 + (14) x 7, which becomes 715 = 5 + 98 = 103
We will work through a few test questions:
Find the nth term for the following sequence - 100, 90, 80, 70 ...
- The first term is 100
- The common difference is -10
- We will apply this to the formula:
- an = a1 + (n - 1)d
- an = 100 + (n - 1)-10
- an = -10n + 110
Find the nth term for the following sequence - 24, 32, 40, 48 ...
- The first term is 24
- The common difference is 8
- We will apply this to the formula:
- an = a1 + (n - 1)d
- an = 24 + (n - 1)8
- an = 8n + 16
Continue an arithmetic sequence
A common question regarding an arithmetic sequence is to continue the example sequence.
Calculate the next 3 terms: 3, 7, 11, 15, 19 ...
- We can find the common difference by deducting one term from the following term e.g. 7 - 3 = 4
- Add the common difference to the final term to reveal the next term: 19 + 4 = 23
- Repeat the pattern to find the 3 terms: 19 + 4 = 23, 23 + 4 = 27, 27 + 4 = 31
You may also be given an example with negative terms. The same rule applies but this time you will add together negative values rather than positive ones to find the common difference.
Calculate the next 3 terms: -2, -5, -8, -11, -14 ...
- Deduct consecutive terms from the arithmetic sequence. Remember to deduct the smaller value from the greater value e.g. -5 - (-2) = -3
- We now know the difference between consecutive terms is -3. Next, we add the common difference to the final term: -14 + -3 = -17
- Rinse and repeat step two to find all 3 terms: -14 + -3 = -17, -17 + -3 = -20, -14 + -3 = -23
There may also be questions about arithmetic sequences with decimal places as well as with fractions. The same process above will work with these sequences:
Calculate the next 3 terms: 0.2, 1, 1.8, 2.6, 3.4 ...
- Deduct the first consecutive terms to find the common difference: 1 - 0.2 = 0.8
- Add the common difference (0.8) to the final term and repeat to find all 3 terms: 3.4 + 0.8 = 4.2, 4,2 + 0.8 = 5, 5 + 0.8 = 5.8
Calculate the next 3 terms: 1/2, 1 1/4, 2, 2 3/4, 3 1/2, 4 1/4 ...
- Deduct the first consecutive terms to find the common difference: 1 1/4 - 1/2 = 3/4
- Add the common difference (3/4) to the final term and repeat to find all 3 terms: 4 1/4 + 3/4 = 5, 5 + 3/4 = 5 3/4, 5 3/4 + 3/4 = 6 1/2
Find missing numbers in an arithmetic sequence
A common Maths GCSE question is to find missing numbers in an arithmetic sequence. For example, 5, 8, 11 ... 23. To find missing numbers, we need to use the common difference.
It's not very challenging to fill in the example above (14, 17, 20). However, this becomes more challenging when the sequence has large or otherwise awkward terms.
To find the missing numbers, we need to take the following steps:
- Find the common difference by deducting consecutive terms.
- We can then do either of the following:
- Add the common difference to the last term before the missing value.
- Deduct the common difference from the first term after the missing value
- Repeat step two until all missing values have been calculated.
We'll run through a few examples:
Find the missing values in this sequence - 0.4, 0.1 ... -0.11:
- Deduct 0.1 from 0.4 and the common difference is revealed to be -0.3
- Add the common difference to the last visible term: 0.1 + -0.3 = -0.2
- Complete the process until all hidden terms are revealed: 0.4, 0.1, -0.2, -0.5, -0.8, -0.11
Find the missing values in this sequence - 1/2, 1 3/4, 3 ... 9 1/4:
- Deduct 1/2 from 1 3/4 and the common difference is revealed to be 1 1/4
- Add the common difference to the last visible term: 3 + 1 1/4 = 4 1/4
- Complete the process until all hidden terms are revealed: 1/2, 1 3/4, 3, 4 1/4, 5 1/2, 6 3/4, 8, 9 1/4
Create an arithmetic sequence
To generate an arithmetic sequence, we need the nth term.
We can discover any term of an arithmetic sequence by using the nth term. We just need to substitute the value of this term into the nth term.
For example, if we are looking for the second term, then n = 2. If we want the fourth term, then n = 4. Where the nth term becomes really helpful is when it is a large value that we can't find easily manually e.g. the 100th term (n = 100),
This is called the position-to-term, where we use the nth term to work out the number of a given term in a sequence.
We'll run through several examples below to generate an arithmetic sequence.
Generate the first 3 terms of the sequence 6n + 8.
- To find the first term, we substitute n = 1 into the nth term: (6 * 1) + 8 = 14
- We substitute n = 2 into the nth term for the second term: (6 * 2) + 8 = 20
- We substitute n = 3 into the nth term for the third term: (6 * 3) + 8 = 26
The formula used to calculate the n term of a sequence is (5a + 2b)n. Solve the first four terms in the sequence.
- To find the first term, substitute n = 1 into the nth term: (5a + 2b) * 1 = 5a + 2b
- Apply the same process to find the first four terms in the sequence: (5a + 2b) * 1 = 5a + 2b, (5a + 2b) * 2 = 10a + 4b, (5a + 2b) * 3 = 15a + 6b, (5a + 2b) * 4 = 20a + 8b
Calculate the sum of an arithmetic sequence
The sum of an arithmetic sequence means the total of all terms added together. For example, let's say we have the following arithmetic sequence: 2, 4, 6, 8, 10. The sum of this sequence is 2 + 4 + 6 + 8 + 10 = 30.
The following is the formula for the sum of the arithmetic sequence:
Sn = n/2 [2a1 + (n – 1)d]
Let's try applying this formula to the following sequence - 2, 9, 16, 23 ... 310. We need to find out the sum of this sequence of numbers.
- a1 means the first term. In the sequence, this is 2.
- d means the common difference. To find this, we subtract the difference between consecutive terms 9 and 2, which is 7.
- n means the number of terms in the sequence. This means we need to discover the last term (310). To do this, we substitute these values in the nth-term arithmetic sequence formula:
- an = a1 + (n−1)d
- 310 = 2 + (7)(n−1)
- 310 = 2 + 7n - 7
- 310 = 5 + 7n
- 315 = 7n
- n = 45
Now that we have these details, we can complete the sum formula in stages:
Sn = 45/2 [2 x 2 + (54 - 1) x 7]
Sn = 22.5 [4 + 308]
Sn = 7020
The sum of the arithmetic sequence is 7020.
The sum of an arithmetic sequence is also known as the arithmetic series. For example, the arithmetic series of the sequence 1, 4, 7, 10 is 22
Geometric sequences
We will touch briefly on geometric sequences (GP). This is also a sequence or progression. Where it differs is that the terms in a geometric progression have a ratio that remains constant called a common ratio. This is shown by a, ar, ar2 where a is the first term and r is the common ratio of the progression.
Geometric sequences can be finite or infinite. You can multiply or divide terms. The common ratio can be both positive and negative in the same way as the common factor for arithmetic sequences.
Take a look at the examples below on geometric progression:
- The first term is 4
- The term-to-term rule is to multiply by 2
- The first four terms are 4, 8, 16, 32
- The first term is 6
- The term-to-term rule is to divide by 2
- The first four terms are 6, 3, 1.5, 0.7
For more information, you can view the Wikipedia article on geometric sequences.
Glossary
- term - Terms are individual components of expressions or equations. As an example, in the expression 10a + 2, 10a is a term as is 2.
This post was updated on 01 Aug, 2023.

