Circle theorems are an important area of Geometry that is studied in GCSE Maths. These theorems help us understand the properties of circles and their parts, including chords, tangents and arcs. This guide will explain the different types of circle theorems, including quiz questions to test your knowledge and help your GCSE Maths revision. If you need further support, TeachTutti provides a list of qualified GCSE Maths tutors to help you understand this topic.
Circle Theorems in Geometry
Circle theorems are statements that show the relationships between different parts of a circle and the angles formed inside or intersecting circles. They help us to solve a wide range of geometric problems and boost our problem-solving skills.
There are several parts to a circle that are important to these theorems:
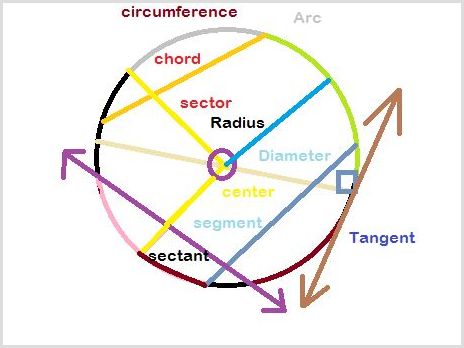
- Radius - A straight line from the centre of the circle to anywhere on its circumference.
- Diameter - A straight line through the centre of the circle, joining two points on its circumference. It's twice the length of the radius.
- Chord - A straight line segment where the endpoints lie on the circle.
- Tangent - A straight line that touches the circle at exactly one point.
- Arc - A part of the circumference of a circle.
- Sector - A part of a circle enclosed by two radii and an arc.
- Segment - A part of a circle is separated from the rest of the circle by a chord.
1
Which statement is true about the diameter of a circle?
The Alternate Segment theorem
The Alternate Segment Theorem describes the relationship between an angle formed by a tangent to a circle and the angle in the alternate segment of the circle. This is the theorem's definition:
The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Imagine a circle with a chord and a tangent that touches the circle at one of the chord's endpoints. The angles formed here may seem unrelated. However, this theorem tells us that the angle formed outside the circle (between the tangent and the chord) is equal to the angle formed inside the circle, on the opposite side of the chord. The Angle Segment theorem is useful for solving geometric problems that include circles, tangents and chords.
For a broader understanding of how circle theorems fit into the wider world of geometry, consider exploring Khan Academy's comprehensive Geometry course. It's a useful resource to test your knowledge on various geometric problems.
2
In a circle, if the angle formed by a tangent and a chord is 65 degrees, what is the angle in the alternate segment?
Angle at the Centre Theorem
The Angle at the Centre Theorem helps us understand the relationship between angles at the centre of a circle and angles at the circumference. We use this theorem to solve problems related to circle angles and arc lengths. The theorem states:
The angle subtended at the centre of the circle by an arc is twice the angle subtended at the circumference by the same arc.
Breaking it down
Imagine two points on the circumference of a circle that are connected by an arc. An angle is formed at the centre of this circle by lines drawn from the two points to the centre. Another angle is formed at a point on the circumference, on the opposite side of the arc. The Angle at the Centre Theorem tells us that the central angle is exactly twice as large as the circumference angle. This relationship holds for any point on the circumference.
Practical implications
This theorem simplifies calculating unknown angles in circular figures, especially in complex diagrams where multiple circles intersect or overlap. We can use it to establish ratios between angles, making it easier to solve for unknowns. It also underlines how important the centre of a circle is in geometry.
3
If an angle at the centre of a circle subtended by an arc is 120 degrees, what is the size of the angle subtended at the circumference by the same arc?
Angles in the Same Segment theorem
The Angles in the Same Segment theorem shows the consistency of angular measurements in specific segments of a circle. This theorem states that angles in the same segment of a circle are equal to each other.
Let's say we have a circle divided into sections by chords. This theorem says that any angles formed by chords that end on the same arc will always be equal. It simplifies the analysis of complex diagrams involving circles because it allows the deduction of equal angles based solely on their segmental location. It's particularly useful when using cyclic quadrilaterals.
The Angles in the Same Segment Theorem highlights that circles are figures of equal measure and symmetry. This theorem provides a quick method to identify relationships between angles.
4
In a circle, if one angle in a segment formed by a chord is 45 degrees, what is the size of another angle in the same segment formed by a different chord?
Angles in a Semicircle theorem
The semicircle theorem provides a simple insight into the nature of these angles. It states that any angle marked inside a semicircle is a right angle (90 degrees).
Exploring the Angles theorem
Draw a semicircle on a piece of paper. Draw a triangle inside the semicircle so the base of the triangle is the diameter of the semicircle and the apex point lies on the semicircle's arc. The angle formed at this apex will always be a right angle.
This theorem is a specific application of the Angle at the Centre Theorem: the central angle over a diameter (forming a straight line) adds up to 180° so the inscribed angle must be half of that: 90 degrees. This theorem is commonly used in geometric constructions and proofs.
5
If a triangle is inscribed in a semicircle with its base along the diameter, what is the measure of the angle at the apex?
Chord of a Circle
A circle to a chord is a line segment with both endpoints on the circle's circumference. The properties of chords within a circle are governed by specific theorems that reveal deeper relationships. One key property is that chords of equal length subtend equal angles at the centre of the circle.
Understanding Chord Properties
Let's say we have two chords in a circle that are the same length. These chords will subtend angles at the circle's centre equal in measure. We can use this property to show the equality of angles or the lengths of chords.
The perpendicular bisector of a chord always passes through the centre of the circle. This is important in creating circles and solving problems involving the positioning of chords.
6
If two chords in a circle are of equal length, what can be said about the angles they subtend at the centre of the circle?
Tangent of a Circle
The tangent of a circle is a line that touches the circle at exactly one point, known as the point of tangency. A tangent is perpendicular to the radius at the point of tangency.
This perpendicular relationship between a tangent and a radius is important for many geometric proofs and problem-solving techniques. For example, if you know the point where a line touching a circle is perpendicular from the centre to a radius, you can identify that line as a tangent.
The tangent to a circle theorem states that if two tangents are drawn to a circle from an external point, they are equal in length. This property highlights the symmetry in circle geometry and helps us to solve complex problems involving circles and lines.
7
If a line segment is drawn from an external point to touch a circle at one point, making a 90-degree angle with a radius at the point of contact, what is the line segment called?
Cyclic Quadrilateral theorem
Cyclic quadrilateral combines several elements of circle geometry. A cyclic quadrilateral is a four-sided figure (quadrilateral) with all its vertices lying on the circumference of the circle. A key property of cyclic quadrilaterals is that the opposite angles sum up to 180 degrees (supplementary angles).
Exploring Cyclic Quadrilaterals
Imagine drawing any quadrilateral inside a circle so that each corner (vertex) touches the circle's edge. The lines of a quadrilateral don't look connected. However, the rule about opposite angles being supplementary provides a tool for solving geometric problems involving these shapes. It also plays a role in proofs and constructions in circle geometry, giving insights into the relationships between circular and polygonal shapes.
8
Consider the angles in a cyclic quadrilateral. If one angle is 70 degrees, what is the measure of its opposite angle?
Subtended Angles
Subtended angles provide a bridge between linear and circular geometry by examining the angles created by points on the circumference of a circle. A subtended angle is created when two points on a circle's circumference are connected to a third point, either on the circle or inside it. This creates a subtended angle at that third point.
It's important to remember that the angle subtended by an arc at the centre of the circle is twice the angle subtended by the same arc at any point on the circumference.
Understanding Subtended Angles
This theorem highlights the relationship between central angles and those at the circumference. This relationship always remains constant on the same arcIt's useful for solving problems where the measure of an angle at the centre/circumference is known and the other needs to be determined. It extends to situations involving cyclic quadrilaterals, where subtended angles can show unknown angles.
9
If an arc subtends an angle of 80 degrees at the centre of the circle, what is the measure of the angle subtended by the same arc at a point on the circumference?
Conclusion
Circle theorems provide insight into geometry, showing the symmetry that underpins the structures in everyday life. As you continue to study and explore the fascinating world of circle theorems, remember that each theorem opens the door to new ways of thinking and solving problems. With practice and perseverance, you'll find that what once seemed complex becomes manageable and even enjoyable. If you need support revising this topic, TeachTutti provides a list of qualified GCSE Maths tutors.
Having mastered circle theorems, you may be curious about other areas of geometry that use similar concepts, such as trigonometry. To get started, Mathisfun offers an introduction to trigonometry.
Frequently asked questions
They give a foundation for understanding and solving geometric problems involving circles, angles and lines. They are common in various fields, including engineering and architecture.
The number can vary depending on the exam board. Students are normally expected to know 8 - 10 core theorems that cover the fundamental properties of circles and their components.
Yes, circle theorems have many real-life applications, from designing mechanical parts that fit together to calculating distances and angles in navigation and construction projects.
Practice and application is the best approach. Work through problems that require the use of different theorems and try to understand the underlying principles and relationships between the components of a circle.
Glossary
- Arc - A segment of a circle's circumference.
- Chord - A line segment with both endpoints on the circle's circumference.
- Cyclic Quadrilateral - A quadrilateral with all four vertices on the circumference of a circle.
- Diameter - A chord that passes through the centre of the circle, the longest possible chord.
- Radius - A line segment from the centre of the circle to any point on its circumference.
- Segment - A region of a circle bounded by a chord and the arc it subtends.
- Sector - A region of a circle bounded by two radii and the arc between them.
- Subtended Angle - An angle formed by two points on a circle's circumference and a third point, either on the circle or inside it.
- Tangent - A line that touches the circle at exactly one point.
