Factors are whole numbers that divide exactly into another number without a remainder, e.g. 3 and 6 are factors of 12. Multiples are the answer when you multiply a number by a whole number, e.g. multiples of 5 are 5, 10 and 15. They are important in GCSE Maths because we use factors and multiples in numerous topics, such as simplifying fractions, finding prime factors and solving problems involving the Highest Common Factor and Lowest Common Multiple.
In this article, you will learn about factors and multiples, as well as methods to identify them. We will explain prime numbers and techniques for prime factorisation. Examples are included, and you can test your knowledge with questions and answers. This guide is aimed at students doing GCSE Maths revision. It's suitable for all major exam boards, including AQA and Edexcel.
If you need further help understanding this topic, TeachTutti has qualified GCSE Maths tutors who can provide online or in-person tuition to meet your revision needs.
Factors
A factor divides exactly into a larger number. It doesn't leave a remainder after a decimal digit. Understanding factors helps us with various problems, including simplifying fractions, solving ratios and finding the Highest Common Factor.
If you have two numbers that you multiply together to make a larger number, these two numbers are both factors. For example, in 3 x 4 = 12, 3 and 4 are both factors of 12.
You can reverse this process by finding numbers that divide cleanly into 12 by starting at 1 and gradually increasing the factors:
- 1 × 12
- 2 × 6
- 3 × 4
The full list of factors for 12 is 1, 2, 3, 4, 6 and 12. These are called factor pairs because they work in twos to create the value: (1 and 12), (2 and 6), (3 and 4).
The following are useful tips to remember about factors:
- 1 is a factor of every number
- A number is always a factor of itself, e.g. 12 is a factor of 12
- A factor is always a whole number. You can't have a decimal or a fraction
- A prime number only has two factors: 1 and the number itself
Try to divide a number to find out if it's a factor. This is a factor if you can find an integer with no remainder. For example, 5 is not a factor of 8 because 8 / 5 = 1.6
Multiples
A multiple is when you multiply a number by a whole number. You multiply the number by itself and increment the number of times. Multiples never stop. There is no largest multiple because you keep incrementing the number by which you multiply the value. Multiple examples include the following:
- Example 1 - The multiples of 4 are 4, 8, 12, 16, 20, etc
- Example 2 - The multiples of 6 are 6, 12, 18, 24, 30, etc
- Example 3 - The multiples of 10 are 10, 20, 30, 40, 50, etc
- Example 4 - The multiples of 15 are 15, 30, 45, 60, 75, etc
The key difference between factors and multiples is that factors are numbers that divide into another number exactly. Meanwhile, multiples are the results of multiplying. For instance, 12 is a factor of 24 and 24 is a multiple of 12. Watch that you don't confuse these terms because a number appears in both lists. For example, 12 is a multiple of 4 (4 x 3), while 4 is a factor of 12. The direction of the relationship is crucial.
Every number is a multiple of itself, as multiplying by 1 gives you the same number, e.g. 15 x 1 = 15. Zero is also a multiple of every number, since anything multiplied by 0 is 0. Multiples help us solve problems that include the Lowest Common Multiple, which is discussed later. It also helps calculations with repeated events, synchronised timing, or finding the smallest number that two other numbers will divide into.
Prime Numbers and Prime Factorisation
A prime number is a number that has only two factors: itself and 1. The only way it can be divided without a remainder is by using these numbers. An example of a prime number is 7: the factors are 1 and 7. 9 is not a prime number because it can be cleanly divided by 3 in addition to 1 and 9.
The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
2 is the only even prime number
Prime numbers are the building blocks of all other whole numbers. With the exception of 1, every whole number can be broken down into a product of prime numbers. This is called prime factorisation.
For example:
- Let's say we have the number 60
- You can break this number down as follows: 60 = 6 x 10
- These factors can be further broken down into primes: 6 = 2 x 3 and 10 = 2 x 5
- The prime factorisation of 60 is 2 x 2 x 3 x 5. You can also write this using powers: 2² x 3 x 5
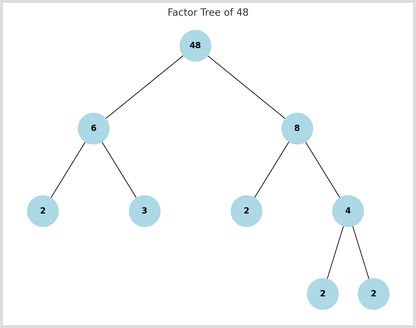
A factor tree visually shows the prime factorisation of a number:
- Let's use the number 48 as an example.
- Divide 48 into any two factors, e.g. 6 x 8.
- Break each factor into primes: 6 breaks down into 2 x 3 (both prime numbers), while 8 breaks down into 2 x 4 (4 breaks down further into 2 x 2).
The factor tree would visually look like this:
Prime factorisation helps to find the Highest Common Factor and Lowest Common Multiple, which are discussed below. It is also required in exam questions that feature simplification and number properties.
Highest Common Factor
The Highest Common Factor (HCF) is the largest factor that two or more numbers share. For example:
- The factors of 12 are 1, 2, 3, 4, 6 and 12
- The factors of 18 are 1, 2, 3, 6, 9 and 18
- The common factors in both numbers are 1, 2, 3 and 6
- The HCF is 6
You can find the HCF by listing all the factors for each number. Then all you need to do is pick the largest one they share. If the number is larger, using prime factorisation is more efficient. For example, let's find the HCF for 12 and 18 using the prime factor method:
- 12 = 2² x 3
- 18 = 2 x 3²
- The common prime factors for 12 and 18 are: 2 x 3
- The HCF is 6
The HCF can help in questions that involve sharing, grouping, or dividing items into the largest equal parts. In particular, it can simplify factions. For instance, if we have the fraction 18/24, we can divide the numerator and denominator by the HCF, which is six: 18 / 6 = 3 and 24 / 6 = 4. This means 18/24 simplifies to 3/4.
Lowest Common Multiple
The Lowest Common Multiple is the smallest multiple of two or more numbers. It's the first number that appears for both numbers when listing their multiples.
For example, let’s find the LCM of 4 and 6:
- The initial multiples of 4 are 4, 8, 12, 16, 20 and 24
- The initial multiples of 6 are 6, 12, 18, 24 and 30
- The first common multiple for both 4 and 6 is 12
- The LCM is 12
When the numbers are large, use prime factorisation to find the LCM. Rather than taking the lowest powers of common primes, you must take the highest powers of all primes that appear as multiples. For example, let's find the LCM of 12 and 18:
- Prime factorisation of 12 = 2² x 3
- Prime factorisation of 18 = 2 x 3²
- Take the highest powers of each: 2² (for 12) and 3² (for 18)
- The LCM is 36 (2² x 3² = 4 x 9)
LCM problems in exam questions will typically take the form of real-life situations about timing or schedules. For example, how long will it be before traffic lights flash together if one set flashes every 6 seconds and the other set flashes every 8 seconds? You can find the answer by finding the LCM of 6 and 8.
List of quiz questions
1
What number is not a factor of 24?
2
Which number is a multiple of 7?
3
What are the prime factors of 30?
4
What is the Highest Common Factor of 20 and 50?
5
What is the Lowest Common Multiple of 6 and 8?
6
Which number is a factor of both 36 and 48?
7
What is the prime factorisation of 100?
8
Which of the following is true?
9
What is the Lowest Common Multiple (LCM) of 5 and 15?
Conclusion - Multiples and factors
Factors and multiples are the foundation for topics that include simplifying fractions, using ratios and solving problems that involve HCF and LCM. Being able to break a number into its factors or find a multiple will help with many exam questions in GCSE Maths.
This article has explained what factors and multiples are, how to recognise prime numbers, how to use prime factorisation and the Highest Common Factor and Lowest Common Factor. For further reading, Third Space Learning have explored a factor tree in more detail. You can also test yourself with past paper questions on factors, multiples and primes by Maths Genie.
If you need more help on this or related topics, TeachTutti has GCSE Maths tutors. Every tutor is DBS checked, and you can learn in person or online. Tutors are vetted and will adapt lessons to meet your specific needs.

