Understanding different 3-dimensional shapes is part of the GCSE Maths curriculum. It is a shape with three dimensions: length, width and height - for example, cubes, cylinders, cones and prisms.
This article will explain how to identify common 3d shapes and their properties, such as faces, edges and vertices. We will list formulas to calculate surface area and volume. This GCSE Maths revision guide will also explain what a net is for a 3d shape. Exam questions and answers are included to test your knowledge. It is suitable for all major exam boards, including Edexcel.
If you need help learning this topic, TeachTutti has qualified GCSE Maths tutors for in-person or online tuition.
Properties of 3D Shapes
A 3D shape is short for a "three-dimensional shape". It is a solid object that unsurprisingly has three dimensions: length, width and height. This contrasts with a flat 2d shape, such as a square or circle. A 3d shape has depth and takes up space. It can be held or built. We see them everywhere in the world around us: boxes, footballs, cans of food, pyramids, etc.
There are three key features in a 3D shape. Recognising these terms will help with geometry questions, such as labelling a shape:
- Faces - the flat or curved surfaces that we can see on the outside of the shape
- Edges - where two faces meet, such as the corner of a box
- Vertix - the places where the edges meet on the shape. The plural is vertices
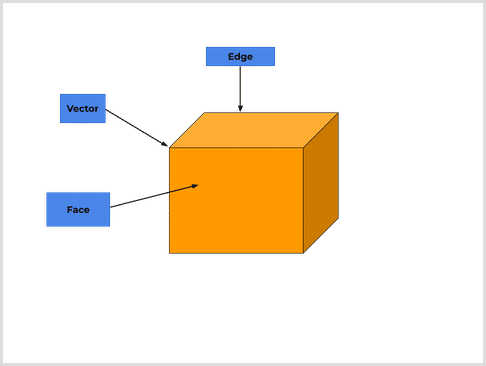
Here are a few examples applied to common 3d shapes:
- Cube - There are 6 faces, 12 edges and 8 vertices. Every face is square (see the image above and count to see if you can match these figures).
- Cylinder - There are 2 flat circular faces on the top and bottom. There is one curved surface stretching around the length. There are no vertices.
Types of 3D Shapes
There are certain 3D shapes that you are more likely to encounter in GCSE Maths. The questions may ask about nets, surface area, volume, or identifying properties. Being familiar with the names and features of these shapes is essential.
We have described these shapes below. Each has its unique properties, including the number of faces, edges and vertices.
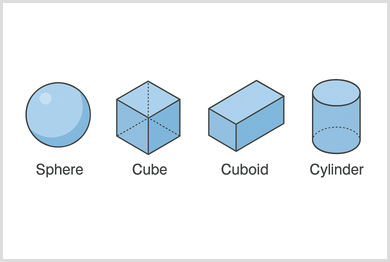
Cube
- 6 square faces
- 12 edges
- 8 vertices
- All edges are the same length
Cuboid
- Six faces that are rectangular
- 12 edges
- 8 vertices
- It is essentially a stretched cube. Examples include a box and a brick
Sphere
- 1 curved surface
- 0 edges
- 0 vertices
- For example, a football or a marble
Cylinder
- 2 flat circular faces and 1 curved surface
- 2 edges
- 0 vertices
- For example, a can of soup
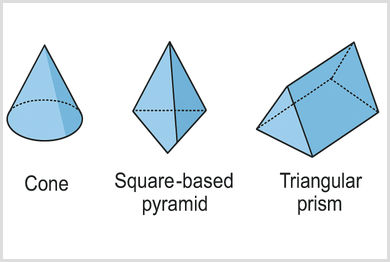
Cone
- 1 flat circular face and 1 curved surface
- 1 edge
- 1 vertex (the point at the tip)
- For example, an ice cream cone
Square-based Pyramid
- 1 square base and 4 triangular faces
- 8 edges
- 5 vertices
- For example, the pyramids in Egypt
Triangular Prism
- 2 triangular faces and 3 rectangular faces. The two end faces are identical in shape and size
- 9 edges
- 6 vertices
- For example, a Toblerone chocolate bar
Nets of 3D Shapes
A net is what a 3d shape looks like when you unfold it, effectively turning it into a flat 2d shape. For example, imagine perfectly disassembling a box containing a package you received in the mail. The net of a shape helps us to see how it was assembled. It is particularly useful for working out surface area.

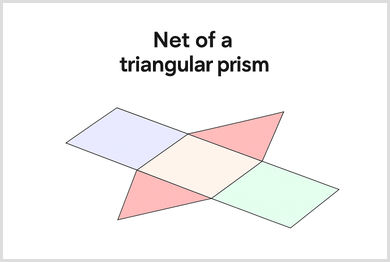
For example:
- Cube - The net of a cube shows 6 squares. They are arranged in a cross pattern
- Triangular prism - This net has two triangles and three rectangles
Exam questions about 3d nets may ask you to identify: which net matches a 3d shape or vice versa; draw the net that a 3D shape would fold into; use a net to calculate the total surface area. These questions can be designed to trick you, so it's a good idea to practice a variety.
Calculate surface area & volume
Every 3D shape has two metrics you will typically be required to calculate: its surface area and volume.
- Surface area - This is the total area of all the faces of the shape
- Volume - This is the total amount of space the shape takes up inside
Key formulas
Every shape has formulas that you will be expected to memorise for your examinations. We have covered the formulas for key shapes below. When using these formulas in your workings, make sure you:
- Use the right units (e.g. cm² for area and cm³ for volume)
- Label your answers clearly
- Round only at the end if required
Cube
- Surface area: 6 × side²
- Volume: side³
Cuboid
- Surface area: 2(lw + lh + wh)
- Volume: length × width × height
Cylinder
- Surface area: 2 × pi × r^2 + 2 × pi × r × h
- Volume: pi × r^2 × h
Sphere
- Surface area: 4 × pi × r^2
- Volume: (4/3) × pi × r^3
Cone
- Surface area: pi × r^2 + pi × r × l (where l is the slant height)
- Volume: (1/3) × pi × r^2 × h
Pyramid
- Surface area: base area + area of triangular faces
- Volume: (1/3) × base area × height
Example question
A cylinder has a radius of 3 cm and a height of 5 cm. What is its volume?
To find the answer to this problem, do the following:
- Use this formula: pi × r^2 × h = pi × 3^2 × 5 = pi × 9 × 5 = 45 × pi
- This means the volume equals approximately 141.37 cm³ (if you use pi = 3.14)
Working with dimensions - Real-world uses
Sometimes you may question the relevance of topics in the GCSE Maths curriculum to the world around you. This is certainly not the case with 3D shapes, which we see everywhere in real life. This is especially the case in jobs that involve designing, building or measuring things:
- Architecture and design - 3D shapes are commonly used by architects to design buildings, bridges and stadiums. For example, domes, cones and triangular prisms often feature in structures to ensure they are strong and stable.
- Packaging and manufacturing - Companies need to calculate the surface area when designing packaging. This is so they know how much material is required and the volume that the product can fit inside. For example, designing cereal boxes, cans or tubes.
- Engineering and construction - Engineers often use cylinders (pipes), cubes (foundations) and spheres (tanks) to build machines or structures. Calculating volume and surface area is an important aspect of planning as it allows engineers to estimate costs, materials and performance.
GCSE-Style Quiz
1
Which 3D shape has one curved surface and one flat face?
2
How many edges does a triangular prism have?
3
A cube has a side length of 5cm. What is its volume?
4
Which shape does this net fold into?

5
What is this shape?

6
The area of the triangle in this shape is 10 cm² and the length is 8 cm. What is the volume?
Conclusion - 3d shapes revision
3D shapes are everywhere in the world around us. From designing buildings to packing boxes, understanding shapes like cubes and cylinders helps us with problem-solving and practical thinking.
This article has explored the main types of 3D shapes, including how to calculate surface area and volume. We have looked at the nets of shapes, formulas to memorise for key shapes and tested your knowledge with quizzes.
For further reading, you can read ThirdSpaceLearning's article on the volume formula for 3D shapes. SaveMyExams has past paper questions on 2D and 3D shapes to test your knowledge on a variety of questions.
If you need more support learning this topic, TeachTutti has verified GCSE Maths tutors who can offer bespoke tuition to suit your needs, such as preparing revision notes. Lessons can be online or in-person, and every tutor has an enhanced DBS check.
This post was updated on 09 Jul, 2025.

